Sudoku Solver
Sudoku is a puzzle game where you fill a grid with numbers. In the classical version, the puzzle is a 9x9 grid. The task is to fill this grid, such that in each row, each column and each of the nine 3x3 subgrids, the numbers of 1 to 9 appear only once.
The starting point of each puzzle is a set of prefilled numbers, where the count of given numbers usually determines the degree of difficulty. In a good sudoku, the initial numbers can only result in a unique solution. The following 3 puzzles are such examples:
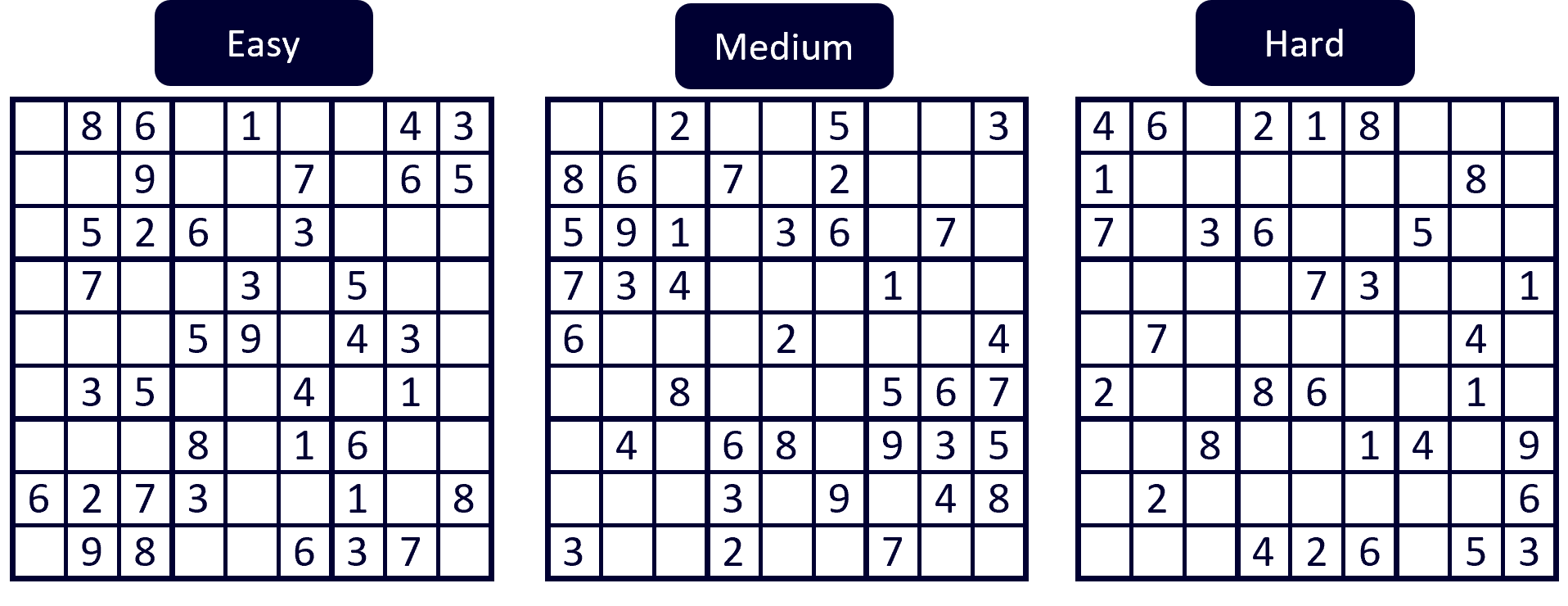
Solver
When solving a Sudoku puzzle by hand, one has to apply certain logics to infer which number can be placed in which field with absolute certainty. A brute-force approach trying all combinations of numbers is not feasible for a human. Also, reversing wrongly placed numbers is very cumbersome.
Whereas a machine could easily brute-force all combinations, it is not efficient to do so. Defining all possible logics a human would apply to achieve absolute certainty about the positioning of numbers is probably also not efficient and will not make the code understandable.
A good solution for a machine is to make best guesses. And if these guesses do not end up in a solution, there needs to be a logic to reverse them. This concept is called backtracking.
Algorithm
Define the initial grid for the Sudoku puzzle.
For all empty fields in the grid, try:
- Place a valid number in the field and continue with the next empty field
- If there is no valid number, return to an earlier stage
- If there are no empty fields left, it is a solution
(See the code at the end of the post)
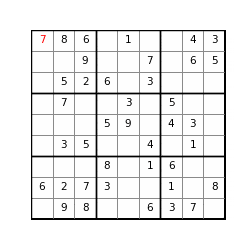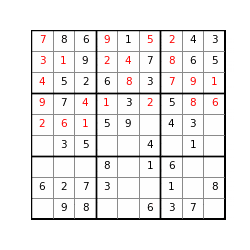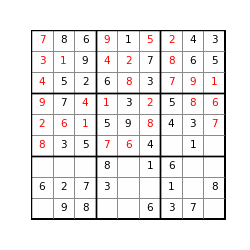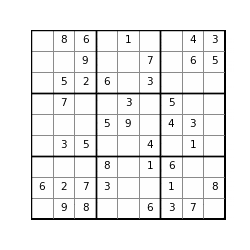
Code
# Check if a number x can be placed in field[r, c] of the grid
def check_field(r, c, x):
global m
# Check the row
for i in range(0,9):
if m[r][i] == x:
return False
# Check the column
for i in range(0,9):
if m[i][c] == x:
return False
# Check the box
r_ = (r // 3) * 3
c_ = (c // 3) * 3
for i in range(0,3):
for j in range(0,3):
if m[r_+i][c_+j] == x:
return False
return True
# The solver function - refer to sketched algortihm
def solve_Sudoku():
global m
global i
# Loop trough all rows and columns
for r in range(9):
for c in range(9):
# If the current field is empty
if m[r][c] == 0:
# Find a first number that can be placed in the empty field
for n in range(1, 10):
if check_field(r, c, n):
# Enter value
m[r][c] = n
# Check next cells
solve_Sudoku()
# Reached dead end
m[r][c] = 0
# Could not find a valid number to place in the field
return
# Keep track of the number of solutions
i = i + 1
if print_m:
print(np.matrix(m))
print(i)
# A wrapper function to easily call the solver on multiple puzzles
def solve_Sudoku_bench(m_, print_matrix = False):
global m
global i
global print_m
print_m = print_matrix
m = m_.copy()
i = 0
solve_Sudoku()
# Solve the easy puzzle
m_easy = [
[0, 8, 6, 0, 1, 0, 0, 4, 3],
[0, 0, 9, 0, 0, 7, 0, 6, 5],
[0, 5, 2, 6, 0, 3, 0, 0, 0],
[0, 7, 0, 0, 3, 0, 5, 0, 0],
[0, 0, 0, 5, 9, 0, 4, 3, 0],
[0, 3, 5, 0, 0, 4, 0, 1, 0],
[0, 0, 0, 8, 0, 1, 6, 0, 0],
[6, 2, 7, 3, 0, 0, 1, 0, 8],
[0, 9, 8, 0, 0, 6, 3, 7, 0]
]
solve_Sudoku_bench(m_easy, print_matrix = True)